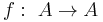Unary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a function
where A is a set. In this case f is called a unary operation on A.
Common notations are prefix notation (e.g. +, −, not), postfix notation (e.g. factorial: n!), functional notation (e.g. sin x or sin (x)), and superscripts (e.g. transpose AT). Other notation exists as well, for example in the case of the square root a horizontal bar over the argument extending the square root sign can indicate the extent of the argument.
Contents |
Unary negative and positive
As unary operations have only one operand they are evaluated before other operations containing them. Here is an example using negation:
- 3 − −2
Here the first '−' represents the binary subtraction operation, while the second '−' represents the unary negation of the 2. Therefore, the expression is equal to:
- 3 − (−2) = 5
Technically there is also a unary positive but it is not needed since we assume a value to be positive:
- (+2) = 2
Unary positive does not change the sign of a negative operation:
- (+(−2)) = (−2)
In this case a unary negative is needed to change the sign:
- (−(−2)) = (+2)
Computer programming
Unary operators (called "monadic" in APL) are also used in programming languages.
C family of languages
In the C family of languages, the following operators are unary:
- Increment:
++x, x++ - Decrement:
−−x, x−− - Address:
&x - Indirection:
*x - Positive:
+x - Negative:
−x - One's complement:
~x - Logical negation:
!x - Sizeof:
sizeof x, sizeof(type-name) - Cast:
(type-name) cast-expression
Other languages
Windows PowerShell
- Increment:
++$x, $x++ - Decrement:
−−$x, $x−− - Positive:
+$x - Negative:
−$x - Logical negation:
-not $x - Invoke in current scope:
.$x - Invoke in new scope:
&$x - Cast:
[type-name] cast-expression
See also
References
- Matt Insall, "Unary Operation" from MathWorld.